あっ, どーも僕です.
後輩(男)から, ラグランジェ補間法の導出の仕方を聞かれたんですが, もう何度もやっていて正直めんどくさいので, ここに簡単に書いておきます.
すでに, このブログになんどか登場していますが, ラグランジェ補間法とは任意の点を通る関数(一価)を設定する手法です. 数値積分を習えば必ず出ててくる極めて一般的な手法です.
任意の n+1 点を次のように設定します. ,%20%5Ccdots,%20(x_i,%20y_i),%20%5Ccdots,%20(x_n,%20y_n).png)
このとき, 定義とかは省略しますが, 設定した点を通りそうな関数を次のように考えます.
%3Dl_0(x)y_0+%5Ccdots+l_i(x)y_i+%5Ccdots+l_n(x)y_n.png)
上の式のなかで 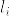 を
を 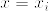 のときに1, それ以外の設定した点で0となるように決めればラグランジェ補間法が得られます.
のときに1, それ以外の設定した点で0となるように決めればラグランジェ補間法が得られます.
まず, 因数定理から次式を得ます. 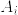 は定数です.
は定数です.
%3DA_i%5Cdisplaystyle%5Cprod_%7Bj%5Cneq%20i%7D(x-x_j).png)
また, 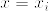 のときに1という条件から次式を得ます.
のときに1という条件から次式を得ます.
%3DA_i%5Cdisplaystyle%5Cprod_%7Bj%5Cneq%20i%7D(x_i-x_j)%3D1.png)
よって, 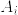 が得られますので,
が得られますので, 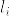 が条件通りに設定出来ます.
が条件通りに設定出来ます.
%5Cright%5C%7D%5E%7B-1%7D.png)
すべての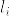 を求めればラグランジェ補間法の完成です. まとめるとこのような式になります.
を求めればラグランジェ補間法の完成です. まとめるとこのような式になります.
%26%3D%26%5Cfrac%7B(x-x_1)(x-x_2)%5Ccdots(x-x_N)%7D%7B(x_0-x_1)(x_0-x_2)%5Ccdots(x_0-x_N)%7Dy_0%20%5Cnonumber%20%5C%5C%0A%26+%26%5Cfrac%7B(x-x_0)(x-x_2)%5Ccdots(x-x_N)%7D%7B(x_1-x_0)(x_1-x_2)%5Ccdots(x_0-x_N)%7Dy_1%20%5Cnonumber%20%5C%5C%0A%26+%26%5Ccdots%20%5Cnonumber%20%5C%5C%0A%26+%26%5Cfrac%7B(x-x_0)(x-x_1)%5Ccdots(x-x_%7Bi-1%7D)(x-x_%7Bi+1%7D)%5Ccdots(x-x_N)%7D%7B(x_i-x_0)(x_i-x_1)%5Ccdots(x_i-x_%7Bi-1%7D)(x_i-x_%7Bi+1%7D)%5Ccdots(x_i-x_N)%7Dy_i%20%5Cnonumber%20%5C%5C%0A%26+%26%5Ccdots%20%5Cnonumber%20%5C%5C%0A%26+%26%5Cfrac%7B(x-x_1)(x-x_2)%5Ccdots(x-x_%7BN-2%7D)(x-x_N)%7D%7B(x_%7BN-1%7D-x_0)(x_%7BN-1%7D-x_1)%5Ccdots(x_%7BN-1%7D-x_%7BN-2%7D)(x_%7BN-1%7D-x_N)%7Dy_%7BN-1%7D%20%5Cnonumber%20%5C%5C%0A%26+%26%5Cfrac%7B(x-x_1)(x-x_2)%5Ccdots(x-x_%7BN-2%7D)(x-x_%7BN-1%7D)%7D%7B(x_%7BN%7D-x_0)(x_%7BN%7D-x_1)%5Ccdots(x_%7BN%7D-x_%7BN-2%7D)(x_%7BN%7D-x_%7BN-1%7D)%7Dy_%7BN%7D.png)