Rで指数乱数を使って中心極限定理を感じてみる
エレベーターに酸っぱい匂いが充満してました.
あっ, どーも僕です.
中心極限定理
中心極限定理とは, 同一の確率分布から得られた独立な確率変数の期待値の分布は, 漸近的に標準正規分布に従うように変換できるというあれです.
で, 統計学の本を学びなおしていたら, 昔は理解できなかった多変量中心極限定理を, 今度は理解できたのかなと思ったのでRでシュミレーションしてみました.
シュミレーションは一変量の復習と, 二変量でやってみました(二変量以上はグラフでの表現の仕方がわからない....)
一変量
一変量の場合は, いつ読んだか忘れましたが既に間瀬先生のデータサイエンス入門にベータ分布を利用したものが記載されていたと思うので, ここでは平均値1の指数分布を用いました.
一変量の場合の数式はざくっというと下のっような感じです. めんどくさいので定義域とか記号は細かく説明しませんが, 慣れ親しんでる理解の通りで大丈夫です.
Rのコードと結果がこちら. n = 10 でもあんまりにみえますね.

# ******************************************************************* # 指数分布に従う乱数で中心極限定理を体感する # ****************************************************************** # 一変量 n <- 10 # 十個くらいでは微妙な結果 Nsim <- 10000 X <- matrix(rexp(n * Nsim, 1), nrow = n) # n = 1 ~ 10を全部試すのでscaleは使わない y <- apply(X, 2, cumsum) y <- sweep(y, 1, 1:n, "/") y <- y - 1 y <- sweep(y, 1, sqrt(1:n), "*") # グラフ化 def.par <- par(no.readonly = TRUE) # デフォルトの環境を保存 layout(matrix(1:n, byrow = TRUE, nrow = 2)) for (i in 1:n) { par(mar = c(2, 2, 3, .5)) hist(y[i,], col = "darkgrey", border = "lightgrey", main = paste("n = ", i), cex.main = 2, freq = FALSE) para <- (fitdistr(y[i, ], "normal"))[[1]] #データの最尤推定量 curve (dnorm(x, para[1], para[2]), add = TRUE) curve (dnorm, add = TRUE, col = "darkred") #標準正規分布 } par(def.par) # デフォルトの環境を復帰
二変量
多変量の場合をしてもよいのですが, 二変量以上はどう表現したらいいのかわからないので, とりあえず二変量でやりました. イメージとしては, 分散共分散行列を維持した状態のままのものを, 分散共分散行列の逆行列のCholeski Decompositionsしたもので線形変換して多変量標準正規分布を得るところですね.
多変量中心極限定理を簡単に説明すると, 独立なk次元ベクトル列 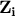 には平均値と分散共分散行列あり,
には平均値と分散共分散行列あり,
と計算できるとします. このとき, 分散共分散行列を維持した多変量中心極限定理は次のようになります.
あとはこれを, 分散共分散行列が単位行列になるように線形変換すればおkって話です. Rで平均値1の指数乱数と平均値2の指数乱数でやってみたのがこちら. nが小さいとうまくいかないのは一変量ですでにわかっていたので, nを大きくしました. まだ正の値が多くでているようですが, 良い感じに二変量標準正規分布になってるかと思います.

# その2 平均1, 2の指数乱数で多変量中心極限定理 # 乱数を発生させて, arrayに保存, 三次元目がサンプル数 M <- c(1, 2) # 指数乱数の平均値ベクトル k <- length(M) # 二変量 n <- 1000 Nsim <- 10000 # X <- array(0, c(k, n, Nsim)) for (j in seq_len(k)) X[j, ,] <- rexp (n * Nsim, 1 / M[j]) # 標準化 result <- matrix(apply(X, c(1, 3), mean), byrow = TRUE, ncol = 2) result <- sweep(result, 2, M, "-") * sqrt(n) B <- t(chol(solve(cov(result)))) result <- t(tcrossprod(B, result)) # グラフ化 library(hexbin) bin <- hexbin(result[,1],result[,2], xbins=50) plot(bin, main="Two-dimensional central limit theorem using random exponents")
%7D%7B%5Csigma%7D%5Cle%20x%5Cright)%3D%5CPhi(x)%5C%5C%0A%5Coverline%7BX%7D_n%3D%5Cfrac%7B1%7D%7Bn%7D%5Csum_%7Bi%3D1%7D%5EnX_i%5C%5C%0A%5Cdisplaystyle%5Cfrac%7B%5Csqrt%7Bn%7D%5Cleft(%5Coverline%7BX%7D_n%20-%20%5Cmu%5Cright)%7D%7B%5Csigma%7D%5Cstackrel%7B%5CL%7D%7B%5Clongrightarrow%7DZ%5Csim%20N(0,%201).png)
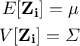
%5Cstackrel%7B%5CL%7D%7B%5Clongrightarrow%7D%7B%5Cbf%20W%7D%5Csim%20N_k(%7B%5Cbf%7B0,%20%5CSigma%7D%7D)%5C%5C%0A%7B%5Cbf%20%7B%5Coverline%7BZ%7D%7D%7D%3D%5Cfrac%7B1%7D%7Bn%7D%5Csum%5En_%7Bi%3D1%7D%5Cbf%7BZ%7D_i.png)