Rで95%信頼区間の95%具合を感じてみる
あっ, どーも僕です.
95%信頼区間のシュミレーション
t検定における信頼係数αとした信頼区間のお話.
わたしが通っている学科は土木系なので授業は力学か, 環境系の話に偏ってしまい統計学の授業が少ないです. 学部の時には確か信頼性設計以外の普通の統計学講義はひとつしかなかったと思います.
まぁ, それを言い訳していけないのですが, 正直にいうと後輩に信頼区間を聞かれたときにうまく説明できませんでした. 恥ずかしいです.
そこで今回はRで95%信頼区間の95%具合を感じてみるシュミレーションをしてみました. で, 信頼区間のイメージが間違っているとここから先を読んでも意味ないので, とりあえずわたしの信頼区間についての認識を先に示しておきます.
信頼係数1-αの信頼区間とは, 母数を含んだ区間を推定できる確率が1-αとなること. つまり, 信頼係数.95のときに信頼区間を100回推定すると, およそ5回は区間内に母数を含んでいない.
....あっているのかな??ポイントは確率的なのは母数でなくて信頼区間だってことだと思うのですが.
ってことで, シュミレーションしましょう. やるのはt検定における母平均の信頼区間の推定です. t検定をざっと説明すると, まず確率変数 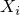 は独立で同一な正規分布に従うとします.
は独立で同一な正規分布に従うとします.
このとき, t分布に従う検定統計量は不偏推定量を用いて次のようになります.
この検定統計量を用いると水準αの両側検定において次が成り立ちます. tはt値です.
で, これを展開すれば母平均μの信頼係数1-αの信頼区間が推定されます.
わたしの理解が正しければ, この区間を100回推定すれば母平均を5回は含んでいない区間を推定しているはず!!
母平均を10にしてRで推定を100回行なってみたのがこちら. 線の長さが推定された区間で緑が成功で, 橙が失敗です. 横軸は何試行目かを表しています. 確かに, 5回失敗しているので, たぶん正しい理解のもとでシュミレーションでいていると思います.

# *************************************************************************************** # 95%信頼区間は「μの分布の95%区間」という意味でなく, #「95%の確率でμを含む区間になっている」という意味である. # つまり, 確率的なのはμじゃなくて, 区間なので100回区間推定すれば5回真値を含んでいない区間となる # 注意:ベイズではμの分布を推定するので, 信頼区間の意味が違う # 各パラメータ alpha <- .05 n <- 10 Nsim <- 100 mu <- 10 ; sigma <- 5 set.seed(78) Z <- matrix (rnorm (n * Nsim, mu, sigma), nrow = n) # シュミレーション!! M <- colMeans (Z) tmp <- apply(Z, 2, sd) / sqrt (n) * qt (1 - alpha * .5, df = n - 1) upper <- M + tmp lower <- M - tmp result <- matrix (c (upper, lower), nrow = Nsim) error <- upper < mu | lower > mu fails <- sum (error) # グラフ col = brewer.pal(2, "Set2") matplot (seq.int (Nsim), result, type = "n", col = col, lwd = 3, ylab = "", lty = 1, las = 1, cex.axis = 2, cex.lab = 2, , xlab = "", bty = "o", tcl = .5, cex.main = 2, main = paste("Number of failtures = ", fails)) segments (seq.int(Nsim), upper, seq.int(Nsim), lower, col = col[1:2][error + 1], lwd = 3) abline (h = mu, col = "darkgrey")
まとめとして, 検定関数風に書くと, 標本平均を引数にとる区間Iを定義すれば信頼区間の意味はこんなこんな感じにかけるのかな.
%5Cequiv%5Cleft%5C%7Bx%20%5Cin%20R%20%5Cquad%20%7C%20%5Cquad%20%5Cleft(%5Coverline%7BX%7D_n%20-%20%5Cfrac%7B%5Ctilde%7B%5Csigma%7D_n%7D%7B%5Csqrt%7Bn%7D%7Dt(n-1,%20%5Calpha%20/2)%20%3C%20x%0A%3C%20%5Coverline%7BX%7D_n%20+%20%5Cfrac%7B%5Ctilde%7B%5Csigma%7D_n%7D%7B%5Csqrt%7Bn%7D%7Dt(n-1,%20%5Calpha%20/2)%5Cright)%5Cright%5C%7D.png)
%20%20%5Cquad%20i%20%3D%201,%20...,%20n.png)
%5E2%5C%5C%0AT_s%5Cequiv%5Cdisplaystyle%5Cfrac%7B%5Csqrt%7Bn%7D(%5Coverline%7BX%7D_n%20-%20%5Cmu)%7D%7B%5Ctilde%7B%5Csigma%7D_n%7D%20%20%5C%5C%0A.png)
%7D%7B%5Ctilde%7B%5Csigma%7D_n%7D%5Cright%7C%3Ct(n-1,%20%5Calpha%20/%202)%5Cright)%3D1-%5Calpha%5C%5C.png)
,%20%5Cquad%5Coverline%7BX%7D_n%20+%20%5Cdisplaystyle%5Cfrac%7B%5Ctilde%7B%5Csigma%7D_n%7D%7B%5Csqrt%7Bn%7D%7Dt(n-1;%5Calpha%20/%202)%5Cright)%5C%5C%0A.png)
%5Cequiv%5Cleft%5C%7B%5Cbegin%7Barray%7D%7Bcc%7D%201%20%26%20%5Cmu%5Cin%20I(%5Coverline%7BX%7D_n)%5C%5C%20%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%200%20%26%20%5Cmu%5Cnotin%20I(%5Coverline%7BX%7D_n)%5Cend%7Barray%7D%5Cright..png)
]%3D1-%5Calpha.png)